As we know, the index is used to provide an ordered indexed data.

However, it is not possible to store the indexed data sequentially because an insert statement may need to move large amounts of data to make room for the new one which is time-consuming.

In order to solve this problem, database use doubly linked list and search tree.

Doubly linked list

Index Leaf Node

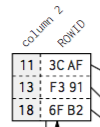
Each leaf node is stored in a database block or page which is database’s smallest storage unit.

One leaf node consist of index entry.

Leaf Nodes

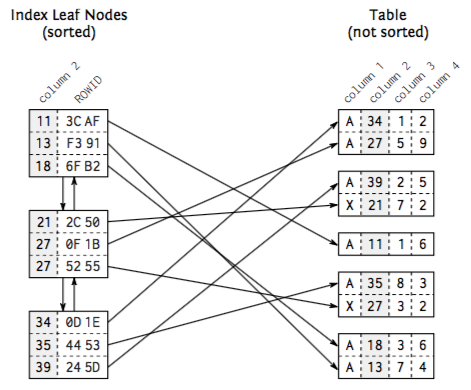
Index leaf nodes are connected by doubly linked list, such that if there is new node inserted, database just need to change the pointer without moving index leaf nodes. As a result, they are stored in an arbitrary of disk.

Search Tree

B-Tree

B-Tree is the abbreviation of Balanced Search Tree. Its structure looks like :

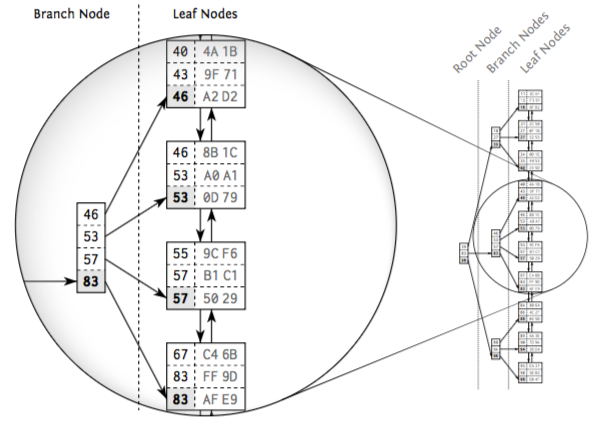
From the above diagram, there are Root Node, Branch Nodes and Leaf Nodes.

Each branch node entry is the biggest value in the respective leaf node.

The same as root node, each root node entry corresponds to the biggest value of each branch node.

Because the tree depth is equal at every position, that is the distance between root node and leaf nodes is the same, so it is called balanced search tree.

B-Tree Traversal

The process of searching indexed data in B-Tree looks like:

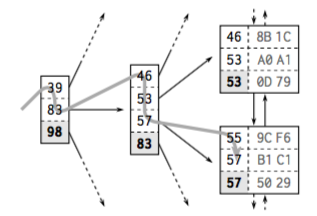
For instance, we need to find data which column2 = 79(column2 is an index data)

  for (Entry rootNodeEntry : rootNode) {

  if( rootNodeEntry.value >= 79 ) {
    
    BranchNode matchedBranchNode = get matched branch node;

    for( Entry branchNodeEntry : matchedBranchNode ) {
    
      if( branchNodeEntry.value >= 79 ) {
      
        LeafNode matchedLeafNode = get matched leaf node;

        for ( Entry leafNodeEntry : matchedLeafNode ) {

          if( leafNodeEntry.value == 79 ) {
          
            Get leaf node entry;
             
          }
        }
        
        LeafNode nextLeafNode = get next leaf node;
        for ( Entry leafNodeEntry : nextLeafNode ) {

          if( leafNodeEntry.value == 79 ) {
          
            Get leaf node entry;
             
          }
        }
      }
    }
  }
}

Efficient

The B-Tree traversal is almost instantly, even on a huge data.

The reason contains:

1. Tree balance. It allows accessing all elements with the same number of steps.

2. Tree depth. Tree depth grows very slowly compared to the number of leaf node. Typically, indexes with millions of records have a tree depth of four or five, while six is hardly ever seen.

Note: the diagrams of this post are from book SQL PERFORMANCE EXPLAINED, author is MARKUS WINAND.